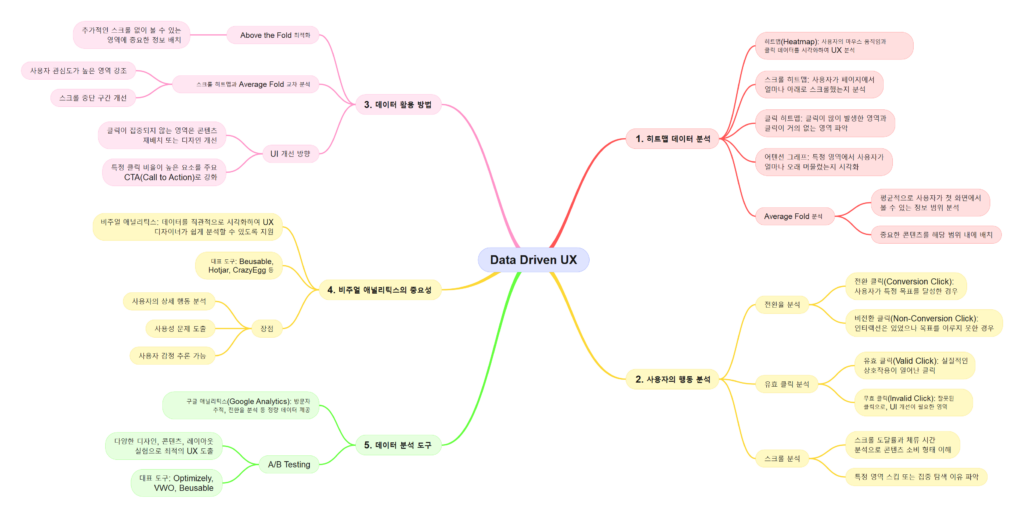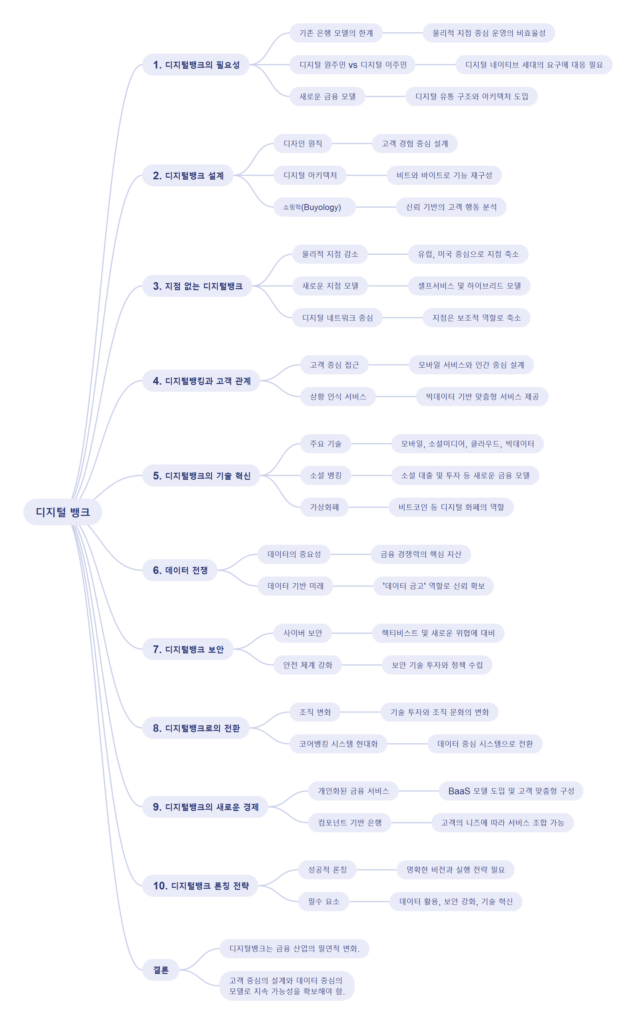
데이터 분석의 중요성
디지털뱅크의 경쟁력은 데이터를 얼마나 효과적으로 분석하고 활용하느냐에 달려 있다. 금융 서비스는 더 이상 단순히 자금의 이동을 관리하는 것이 아니라, 고객의 행동과 니즈를 예측하고 이에 맞춘 맞춤형 서비스를 제공하는 것으로 진화하고 있다. 데이터 분석은 다음과 같은 방식으로 디지털뱅크의 핵심 전략을 지원한다:
- 고객 세분화 데이터 분석을 통해 고객의 행동 패턴과 선호도를 이해하여, 각 그룹에 최적화된 금융 상품과 서비스를 설계한다.
- 위험 관리 신용 점수와 거래 데이터를 기반으로 대출과 같은 금융 상품의 위험을 평가하고 관리한다.
- 예측 분석 고객의 미래 행동을 예측하여 사전적으로 대응할 수 있는 서비스를 제공한다.
데이터 활용의 혁신
디지털뱅크는 데이터를 단순히 저장하는 것이 아니라, 이를 활용해 고객 경험을 혁신적으로 개선하고 있다. 이러한 데이터 활용 방식은 다음과 같다:
- 맞춤형 상품 추천 고객의 소비 패턴과 금융 상황에 맞춘 개인화된 상품과 서비스를 제공한다.
- 실시간 금융 관리 고객이 자신의 재정을 효율적으로 관리할 수 있도록 도와주는 실시간 데이터 기반 도구를 제공한다.
- 비즈니스 인텔리전스 은행 내부 데이터와 외부 시장 데이터를 결합해 전략적 의사결정을 지원한다.
데이터 보안의 중요성
디지털뱅크는 방대한 데이터를 처리하고 저장하기 때문에 보안 문제는 그 어느 때보다 중요하다. 고객 데이터의 안전성을 보장하기 위한 기술적, 조직적 노력은 디지털뱅크의 신뢰도를 좌우하는 핵심 요소이다. 데이터 보안의 주요 전략은 다음과 같다:
- 암호화 기술 모든 데이터를 암호화하여 외부 침입으로부터 보호한다.
- 다단계 인증 고객 인증 절차를 강화해 불법 접근을 방지한다.
- 실시간 위협 감지 AI 기반의 보안 시스템을 통해 사이버 위협을 실시간으로 탐지하고 대응한다.
데이터 금고로서의 디지털뱅크 역할
디지털뱅크는 단순히 데이터를 저장하는 것이 아니라, 이를 활용해 고객에게 가치를 제공하는 데이터 금고로 변모하고 있다. 이는 고객의 재정 데이터를 안전하게 보관하면서도, 필요한 순간에 이를 기반으로 한 서비스를 제공하는 데 중점을 둔다. 이러한 역할은 다음과 같은 방식으로 구현된다:
- 데이터 통합 플랫폼 고객의 모든 금융 데이터를 한 곳에 통합해 관리할 수 있는 플랫폼을 제공한다.
- 투명성 강화 고객이 자신의 데이터가 어떻게 사용되는지 알 수 있도록 투명성을 보장한다.
- 신뢰 구축 데이터의 안전한 관리와 활용을 통해 고객과의 신뢰 관계를 강화한다.
디지털뱅크의 성공 사례
- BBVA 스페인의 BBVA는 데이터 분석과 AI를 활용해 고객 행동을 예측하고 맞춤형 서비스를 제공하는 데 성공했다.
- Capital One 미국의 Capital One은 데이터 중심의 디지털 혁신으로 고객 경험을 개인화하고, 시장에서 경쟁 우위를 확보했다.
- Ping An Bank 중국의 Ping An Bank는 빅데이터와 AI를 통해 금융 상품의 위험 평가와 고객 맞춤형 서비스를 최적화하고 있다.
결론
디지털뱅크는 데이터를 단순한 자산이 아닌, 고객과 은행 모두에게 가치를 창출하는 핵심 자원으로 활용하고 있다. 데이터 분석, 활용, 보안을 전략적으로 관리함으로써 디지털뱅크는 고객 경험을 혁신하고, 금융 서비스의 새로운 기준을 제시하고 있다. 데이터 금고로서의 역할을 충실히 수행하며, 디지털뱅크는 고객 신뢰를 기반으로 지속 가능한 성장을 이루고 있다.