사용자 경험(UX)을 개선하려면 사용자가 실제로 어디에서 멈추고 무엇을 클릭했는지를 이해해야 합니다. 히트맵은 이와 같은 사용자 행동을 시각화하는 도구로, UX 분석과 개선을 위한 강력한 무기가 됩니다. 이 글에서는 히트맵의 정의, 주요 유형, 그리고 실제 사례와 실질적인 활용 방법을 살펴보겠습니다.
히트맵이란 무엇인가
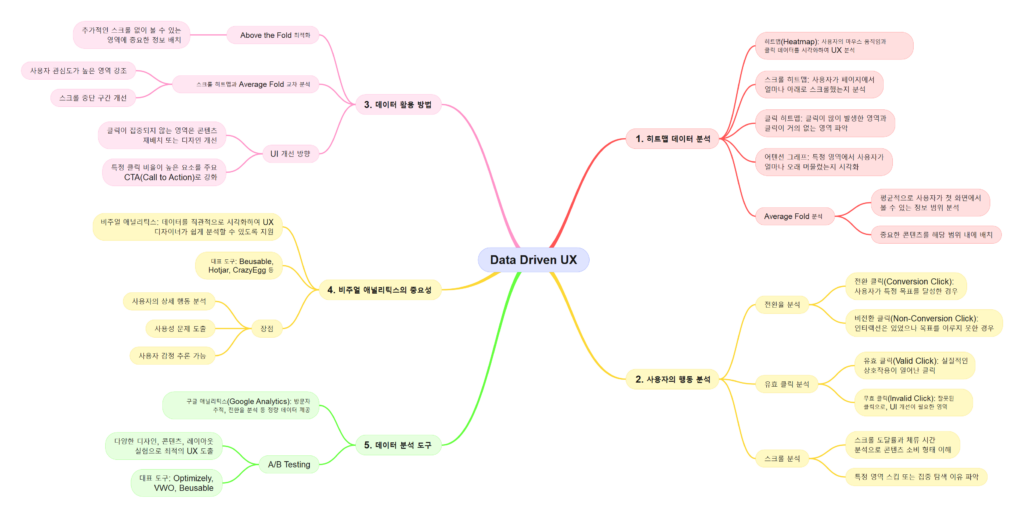
히트맵은 사용자의 행동 데이터를 열 지도 형태로 시각화하여, 웹사이트나 앱에서 사용자들이 주로 어느 영역에 관심을 보였는지 한눈에 보여줍니다. 색상으로 데이터의 강약을 표현하며, 빨간색은 높은 활동 수준, 파란색은 낮은 활동 수준을 나타냅니다. 이러한 시각적 데이터는 사용자의 관심 지점과 행동 패턴을 분석하는 데 필수적입니다.
히트맵의 주요 유형
히트맵은 사용자 행동의 특정 측면을 강조하는 다양한 유형으로 나뉩니다. 대표적인 세 가지 유형은 클릭 히트맵, 스크롤 히트맵, 그리고 어텐션 그래프입니다.
1. 클릭 히트맵
클릭 히트맵은 사용자가 페이지에서 클릭한 위치를 시각화한 것입니다. 클릭이 많이 발생한 영역은 빨갛게, 클릭이 적은 영역은 파랗게 표시됩니다.
- 활용 사례: CTA(Call to Action) 버튼의 위치나 색상이 클릭에 미치는 영향을 파악하고 최적화.
- 실제 활용: 전자상거래 사이트에서 제품 페이지의 “구매하기” 버튼 클릭률을 분석해 버튼 위치를 조정한 결과 매출이 증가한 사례가 있습니다.
2. 스크롤 히트맵
스크롤 히트맵은 사용자가 페이지에서 얼마나 아래로 스크롤했는지를 보여줍니다. 스크롤 도달률이 높을수록 사용자가 페이지 하단까지 탐색했음을 나타냅니다.
- 활용 사례: 중요한 정보가 사용자가 도달하지 않는 하단에 위치하는 문제를 파악.
- 실제 활용: 콘텐츠 블로그에서 사용자가 주요 정보를 보지 못하고 떠나는 문제가 발견되어 중요한 내용을 페이지 상단으로 이동해 체류 시간을 늘린 사례가 있습니다.
3. 어텐션 그래프
어텐션 그래프는 사용자가 페이지 특정 영역에 얼마나 오래 머물렀는지를 분석합니다. 페이지 체류 시간과 스크롤 데이터를 결합하여 주목도를 시각화합니다.
- 활용 사례: 광고 배치 위치의 적정성을 평가하거나, 사용자가 집중하는 콘텐츠 영역을 강화.
- 실제 활용: 미디어 웹사이트에서 어텐션 그래프를 통해 광고 배치 위치를 조정해 클릭률이 30% 증가한 사례가 있습니다.
히트맵 분석의 실제 사례
사례 1: Booking.com
Booking.com은 클릭 히트맵과 어텐션 그래프를 활용해 사용자가 특정 날짜 선택 페이지에서 혼란을 겪고 있음을 발견했습니다. 이를 통해 날짜 선택 UI를 간소화했고, 사용자 만족도와 예약 완료율이 상승했습니다.
사례 2: Shopify 스토어
한 Shopify 스토어는 스크롤 히트맵을 분석해 사용자가 특정 상품 설명까지 스크롤하지 않는 문제를 확인했습니다. 이 데이터를 바탕으로 상품 요약 정보를 페이지 상단에 배치하고 매출이 크게 증가했습니다.
사례 3: 뉴욕 타임즈
뉴욕 타임즈는 어텐션 그래프를 활용해 사용자들이 기사 본문보다 이미지와 동영상에 더 많은 시간을 소비한다는 사실을 발견했습니다. 이 데이터를 기반으로 이미지와 멀티미디어 콘텐츠를 강화하여 체류 시간을 늘렸습니다.
히트맵 분석 실무 팁
1. 적합한 도구 선택
Hotjar, Crazy Egg, Beusable 같은 히트맵 도구를 활용하면 클릭, 스크롤, 어텐션 데이터를 손쉽게 분석할 수 있습니다. 각 도구는 제공하는 기능이 다르므로 필요에 맞는 도구를 선택하세요.
2. 데이터와 맥락 결합
히트맵 데이터는 단독으로 사용하면 한계가 있습니다. 구글 애널리틱스와 같은 분석 도구와 결합하여, 사용자 세그먼트별 행동 패턴을 확인하세요.
3. A/B 테스트 병행
히트맵 분석을 통해 발견한 문제를 해결하기 위해 A/B 테스트를 실행하세요. 예를 들어, CTA 버튼의 색상과 위치를 변경한 버전을 테스트해 어떤 것이 더 나은 성과를 내는지 확인하세요.
히트맵 분석의 중요성
히트맵은 사용자 행동을 이해하는 데 강력한 도구입니다. 클릭 히트맵은 관심이 집중된 영역을, 스크롤 히트맵은 콘텐츠 소비 패턴을, 어텐션 그래프는 사용자 집중도를 보여줍니다. 이 데이터를 활용하면 페이지를 최적화하고, 사용자 경험을 개선하며, 비즈니스 목표를 달성할 수 있습니다.
결론: 히트맵으로 사용자 경험을 개선하라
히트맵은 사용자 경험을 개선하기 위한 필수 도구입니다. 데이터를 분석하여 사용자의 행동을 정확히 이해하고, 이를 바탕으로 UX를 최적화하세요. 작은 디자인 변경도 데이터를 기반으로 한다면 큰 성과를 가져올 수 있습니다.